Answer:
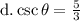
Explanation:
In a right triangle only, the tangent of an angle is equal to its opposite side divided by its adjacent side. If
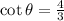 as given in the problem, then
as given in the problem, then
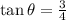 , because
, because
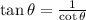 . Therefore, the opposite side of angle theta is 3 and its adjacent side is 4. Thus, the hypotenuse of the triangle must be
. Therefore, the opposite side of angle theta is 3 and its adjacent side is 4. Thus, the hypotenuse of the triangle must be
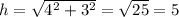 .
.
The sine of an angle in a right triangle is equal to its opposite side divided by its hypotenuse.
Therefore,
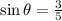 (o/h) and since
(o/h) and since
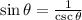 , we have:
, we have:
