Question

!!!!!!Please help ASAP!!!!!

AB and BC form a right angle at their point of intersection, B. If the coordinates of A and Bare (14, -1) and (2, 1), respectively, the y-intercept of AB is 4/3 and the equation of BC is y= 6 X + If the y-coordinate of point Cis 13, its x-coordinate is​

Answer 1

Explanation:

Segments AB and BC intersect each other at 90° at B.

Let the equation of the segment AB → y = mx + b

Here, m = Slope of the line

b = y-intercept

Slope of the line AB passing through A(14, -1) and B(2, 1)

Slope =
`(y_2-y_1)/(x_2-x_1)`

=
`(1+1)/(2-14)`

=
`-(2)/(12)`

=
`-(1)/(6)`

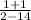
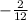
Equation of the line will be,

`y=-(1)/(6)(x)+b`

Since, AB passes through (2, 1)

`1=-(1)/(6)(2)+b`

`b=1+(1)/(3)`

`b=(4)/(3)`

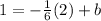
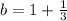
Therefore, y-intercept of AB =
`(4)/(3)`

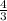
Equation of AB →
`y=-(1)/(6)(x)+(4)/(3)`

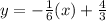
Since, line BC is perpendicular to AB,

By the property of perpendicular lines,

`m_1* m_2=-1`

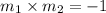
Here,
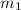`m_1` and
`m_2` are the slopes of line AB and BC respectively.

By this property,

`-(1)/(6)* m_2=-1`

`m_2=6`

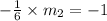
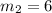
Equation of a line passing through a point (h, k) and slope 'm' is,

(y - k) = m(x - h)

Therefore, equation of line BC passing through B(2, 1) and slope = 6,

y - 1 = 6(x - 2)

y = 6x - 11

Since, line BC passes through C(x, 13),

13 = 6x - 11

6x = 24

x = 4

Therefore, x-coordinate of point C will be, x = 4