Answer:
Explanation:
Segments AB and BC intersect each other at 90° at B.
Let the equation of the segment AB → y = mx + b
Here, m = Slope of the line
b = y-intercept
Slope of the line AB passing through A(14, -1) and B(2, 1)
Slope =
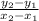
=
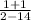
=
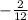
=
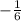
Equation of the line will be,
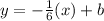
Since, AB passes through (2, 1)
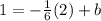
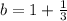
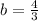
Therefore, y-intercept of AB =
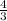
Equation of AB →
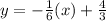
Since, line BC is perpendicular to AB,
By the property of perpendicular lines,
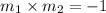
Here,
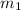 and
and
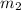 are the slopes of line AB and BC respectively.
are the slopes of line AB and BC respectively.
By this property,
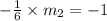
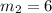
Equation of a line passing through a point (h, k) and slope 'm' is,
(y - k) = m(x - h)
Therefore, equation of line BC passing through B(2, 1) and slope = 6,
y - 1 = 6(x - 2)
y = 6x - 11
Since, line BC passes through C(x, 13),
13 = 6x - 11
6x = 24
x = 4
Therefore, x-coordinate of point C will be, x = 4