Question

May someone please help me on which to graph?

Answer 1

Option (4)

Explanation:

Proportional relationship means,

y ∝ x

y = kx

`k=(y)/(x)`

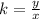
Here, k = proportionality constant

Therefore, if the graph of a line passes through the origin (0, 0) table will represent the proportional relationship.

From table 1,

For a point (1, 2)

`k=(2)/(1)=2`

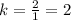
For another point (3, 2)

`k=(3)/(2)=1.5`

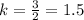
In both the cases 'k' is not same of constant.

Therefore, table (1) is not proportional.

For table (2),

Line passes through (2, 0).

That means there is a x-intercept → (2, 0)

Therefore, table doesn't represent a proportional relationship.

For table (3),

Line passes through a point (0, 1)

It means given line has a y-intercept → y = 1

Therefore, table doesn't represent a proportional relationship.

For table (4),

Line of this table passes through two points (1, 3) and (2, 6)

`k=(3)/(1)=3`

`k=(6)/(2)=3`

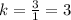
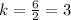
Therefore, proportionality constant for the given table is 3.

Now we can graph table (4).