Answer:
Se vendieron 124 boletos para adultos y 103 boletos para estudiantes.
Explanation:
Un sistema de ecuaciones es un conjunto de ecuaciones con las mismas incógnitas. Un sistema de ecuaciones lineales es un sistema de ecuaciones en el que cada ecuación es lineal.
En otras palabras, un sistema de ecuaciones lineales es un conjunto de dos o más ecuaciones de primer grado, en el cual se relacionan dos o más incógnitas.
Resolver un sistema de ecuaciones significa encontrar valores para las incógnitas que hace verdadera cada una de las ecuaciones.
En este caso, las variables son:
- x: cantidad de boletos para adultos.
- y: cantidad de boletos para estudiantes.
Los boletos para la obra de teatro "Los Miserables" cuestan 15 dólares para adultos y 5 dólares para estudiantes. Si se vendieron 227 boletos y los ingresos fueron de 2,375 dólares, se puede expresar el siguiente sistema de ecuaciones:
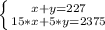
Se elige resolver por el método de sustitución, cuyo primer paso consiste escoger una ecuación y despejar una incógnita en términos de la otra incógnita. En este caso, se despeja la variable "y" de la primer ecuación, obteniendo:
y=227 - x
A continuación se sustituye la expresión hallada en la otra ecuación, para obtener una ecuación con una incógnita y, luego despejar esa incógnita. En este caso, reemplazando la anterior expresión en la segunda ecuación del sistema de ecuaciones:
15*x + 5*(227 -x)= 2375
Resolviendo:
15*x + 5*227 - 5*x= 2375
15*x + 1135 - 5*x= 2375
15*x - 5*x= 2375 - 1135
10*x= 1240
x= 1240 ÷10
x= 124
Finalmente se sustituye el valor hallado en la expresión y=227 - x para despejar la incógnita restante:
y=227 - 124
y= 103
Entonces se vendieron 124 boletos para adultos y 103 boletos para estudiantes.