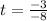Question

A competitive diver dives from a 33-foot high diving board. The height of the diver in feet after 't' seconds is given by u(t) = −16t^2 + 4t + 33. At the moment the diver begins her dive, another diver begins climbing the diving board ladder at a rate of 2 feet per second. At what height above the pool deck do the two divers pass each other? Please answer it quickly, it's for my homework.

Answer 1

`t = 0.375s`

Explanation:

Given

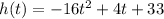`h(t) = -16t^2 + 4t + 33` --- driver 1

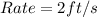`Rate = 2ft/s` -- driver 2

`height = 33ft`

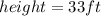
Required

The time they passed each other

First, we determine the function of driver 2.

We have that:

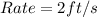`Rate = 2ft/s` and
`height = 33ft`

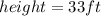
So, the function is:

`h_2(t) = Height - Rate * t`

`h_2(t) = 33 - 2t`

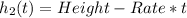
The time they drive pass each other is calculated as:

`h(t) = h_2(t)`

`-16t^2 + 4t + 33= 33 - 2t`

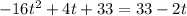
Collect like terms

`-16t^2 + 4t + 2t= 33 - 33`

`-16t^2 + 6t= 0`

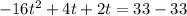
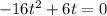
Divide through by 2t

`-8t + 3= 0`

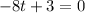
Solve for -8t

`-8t = -3`

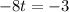
Solve for t

`t = (-3)/(-8)`

`t = 0.375s`