Question

A 1.23 x 10^3 kilogram car is traveling east at 25 meters per second. The brakes are applied and the car is brought to rest in 5.00 seconds. Calculate the magnitude of the total impulse applied to the car to bring it to rest. State the direction of impulse applied to the car.

Answer 1

`\text{Magnitude: }30,000\:\text{Ns},\\\text{Direction: opposite direction of car's movement}}`

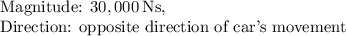
Step-by-step explanation:

*Edit: The original question states a mass of
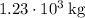`1.23\cdot 10^3\:\text{kg}`. Since the, the poster has corrected it to
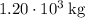`1.20\cdot 10^3\:\text{kg}` and therefore the answers have been change to account for the typo.

The impulse-momentum theorem states that the impulse on a object is equal to the change in momentum of the object.

Therefore, we have the following equation:

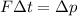`F\Delta t=\Delta p`, where
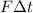`F\Delta t` is impulse (another way to find impulse) and
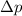`\Delta p` is change in momentum.

Because the car is being slowed to a rest, its final velocity will be zero, and therefore its final momentum will also be zero. Since momentum is given as
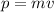`p=mv`, the car's change in momentum is
`1.20\cdot 10^3\cdot 25-0=1230\cdot 25=30,000\:\text{kgm/s}`.

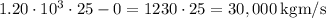As we wrote earlier, this is also equal to the magnitude of impulse on the object. The time it takes to stop the car is actually irrelevant to finding the total impulse. However, if we were to calculated the average applied force on the car, we would need how long it takes to bring it to rest (refer to
`F\Delta t`).

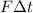The direction of the impulse must be exactly opposite to the car's direction, since we are slowing it to a stop.

Therefore, the impulse on the car is
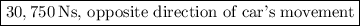`\boxed{30,750\:\text{Ns, opposite direction of car's movement}}`.