Question

I need help with geometry

Answer 1

Answer: C) I and III

Statement 1 and statement 3 contradict

======================================================

Step-by-step explanation:

We'll start with statement 1 and try to build to statement 3, and you'll find that a contradiction happens.

If angle 1 and angle 2 are supplementary, then that must mean
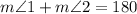`m \angle 1 + m \angle 2 = 180` because the angles can be combined to form a straight angle.

Add the measure of angle 3 to both sides

`m \angle 1 + m \angle 2 = 180\\\\m \angle 1 + m \angle 2+m\angle 3 = 180+m\angle 3`

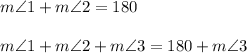
The left side matches with the left side in statement 3, but the right side is a bit off. That
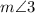`m\angle 3` term needs to be zero, so that the right side boils down to simply 180. However, statement 3 specifically mentions that angle 3 is nonzero. So angle 3 is some positive value.

That's why choice C is the answer.

------------------

Here's an example:

Let's say angles 1 and 2 are 50 and 130 degrees. The order doesn't really matter, but I'll make angle 1 to be the smaller angle.

This means,

`m \angle 1 + m \angle 2 = 180\\\\50 + 130 = 180\\\\`

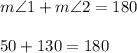
So we've made statement 1 to be true. The angles 50 and 130 are indeed supplementary.

Now let's add some nonzero value to both sides. This will represent the measure of angle 3. If we add say 10 degrees to both sides, then,

`50 + 130 = 180\\\\50 + 130+10 = 180+10\\\\50 + 130+10 = 190\\\\m\angle 1 + m\angle 2 + m\angle 3 = 190\\\\`

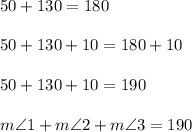
we don't get 180 like we want in the equation of statement 3. This is where the contradiction happens, more or less. One right side is 180, the other right side is 190. The 190 will change if you use some other value for angle 3, but hopefully you can see that it's impossible to add up angles 1 through 3 to get 180. It's only possible if angle 3 were zero degrees.

We can think of it like angles 1 and 2 hog up all the oxygen, and use up 180 points of it, leaving no air for angle 3 to breathe so that's why angle 3 must be 0. Furthermore, it means that a triangle is not possible if exactly two angles are supplementary.

----------------------

Extra info:

• Statements 1 and 2 can coexist just fine without any contradictions happening. If angle 1 is 110 degrees, then that makes angle 2 to be 70 degrees (110+70 = 180). That rules out choice A.
• Statements 2 and 3 are just fine as well, for similar reasoning as above. We can plug in 110 for angle 1, then subtract that from 180 to get 180-110 = 70. Then from here, just ensure that angles 2 and 3 add to 70. So there are infinitely many ways to do this. Choice B can be ruled out.
• Choice D is ruled out because we found choice C to be the answer, ie the contradicting two statements.

Answer 2

C) l and lll

Step-by-step explanation:

m∠1+∠2=180

m∠1+m∠2+m∠3=180

180+m∠3=180

m∠3=0 but m∠3=∦0

-----------------------------------

hope it helps...

have a great day!!