Part A
Answers:
To find the area of the unshaded region, subtract the area of the shaded region from the sum of the areas of the rectangle and semicircle
----------------
Step-by-step explanation:
When it comes to area problems, think of a grid of squares. Let's say we had a 10 by 10 grid of tiny squares (10*10 = 100 total). Now let's say 8 of them are shaded in. There are 100 - 8 = 92 unshaded squares to represent the total area of the unshaded region.
That's effectively what's going on with this problem as well. Sure things get a bit tricky with that curved portion on top, but we can still get an approximation if we use smaller and smaller grid sizes. I recommend using graph paper or graphing software that provides a grid.
========================================================
Part B
Answer: 811
----------------
Step-by-step explanation:
For now, I'm going to ignore the shaded region. I'll come back to it later.
The rectangle is 15 ft by 50 ft. It has an area of length*width = 15*50 = 750 sq ft.
The semicircle up top has an area of
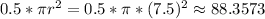 sq ft approximately. The 7.5 is from dividing the diameter in half to get the radius. As the instructions stated, I used the calculator's version of pi.
sq ft approximately. The 7.5 is from dividing the diameter in half to get the radius. As the instructions stated, I used the calculator's version of pi.
The rectangle and semicircle have their areas add to
750+88.3573 = 838.3573
Now we can finally address the shaded region. It is a 3 ft by 9 ft rectangle because "the length is 3 times the width" and the width is 3 ft. This shaded rectangle has area 3*9 = 27 sq ft.
The unshaded region is:
unshaded = total - shaded = 838.3573 - 27 = 811.3573
This rounds to the final answer of 811