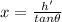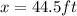Question

Emery looks out their apartment window to the building across the way. The building isknown to be 42 feet tall. The angle of depression from Emery's window to the bottom of the buildingis 27◦, and the angle of elevation to the top of the building is 23◦. Find Emery's distance x from thebuilding across the way.

Answer 1

`x=44.5ft`

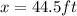
Explanation:

From the question we are told that:

Height
`h=42ft`

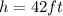
Angle of depression
`\theta=27\textdegree`

Angle of Elevation
`\alpha=23 \textdegree`

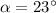
Generally the equation for the vertical distance between Emery's distance x and the bottom of the building is mathematically given by

Since the angle of depression and elevation are given as

27 and 23 respectively

Therefore

Emery's view of the 42 ft building is

`\gamma=23+27`

`\gamma=50 \textdegree`

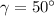
Therefore Emery's distance x to the base of the building h' is

`h'=(27)/(50)*42`

`h'=22.68ft`

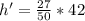
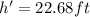
Generally the Trigonometric equation for Emery's distance x is mathematically given by

`x=(h')/(tan\theta)`

`x=(22.68)/(tan 27)`

`x=44.5ft`