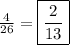Question

PLS HELP ASAP thx>3

In a certain Algebra 2 class of 26 students, 6 of them play basketball and 15 of them play baseball. There are 9 students who play neither sport. What is the probability that a student chosen randomly from the class plays both basketball and baseball?

Answer 1

`(2)/(13)`

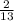
Explanation:

Since there are 26 students in the class and 6 play basketball, 15 play baseball, and 9 play neither, we need to find the intersection (
`\cap`) of the students who play basketball and the students who play baseball to find the number of students who play both.

Since it would appear that we would have 30 students total if we added up the ones who play basketball, baseball or neither, the intersection will be the difference between this total and the actual number of students in the class (26).

Therefore, the number of students who play both sports is
`6+15+9-26=4\:\text{students}`

Since there are 26 students in the class, the probability of randomly choosing one that plays both sports is:

`(4)/(26)=\boxed{(2)/(13)}`