Answer:
There is enough statistical evidence to suggest that the department's claim is not true
Explanation:
The mean weekly sales μ₀ ≤ 2,400 packages
The period over which the weekly sales were measured = Over the last 6 months
The number of stores in the sample, n = 61 stores
The sample mean,
 = 3,593
= 3,593
The sample standard deviation, s = 4919
The significance level = 7% = 0.07
The critical value approach
The null hypothesis, H₀; μ ≤ μ₀
The alternative hypothesis, Hₐ; μ > μ₀
The test statistic is given as follows;
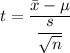
We get;
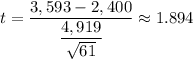
With df = n - 1 = 61 - 1 = 60 at 7% significant level, from a graphing calculator the critical-t, = 1.495598
The p-value at the test statistic is between 0.01 and 0.005
Given that the p-value is less than the significant level, and the test statistic is larger than the critical-t we reject the null hypothesis, that the mean weekly aerosol sale is less than 2,400 packages.
Therefore, there is sufficient statistical evidence to suggest that the departments claim is not true and the mean sales of Aerosols have increased to more than 2,400 packages