Answer:
Attached below
Explanation:
Given that A is a matrix with independent rows
A) Prove
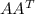 is invertible
is invertible
rank of A = number of rows of Matrix A
This shows that | A | ≠ 0 ( i.e. A has a full rank )
also
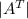 ≠ 0
≠ 0
and
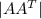 = | A |
= | A |
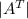 ≠ 0
≠ 0
Hence we can conclude that
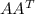 is invertible
is invertible
B) Prove that b is any vector in Col( A )
Attached below is the detailed solution
C) Mapping of Col ( A ) to Row ( A )
b is a non-zero vector hence AXr = 0 ( i.e. there is no solution )
also the kernel of the mapping will be Null
show that mapping preserves the operation
attached below is the detailed solution