Answer:
Given system of inequalities:
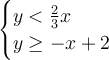
When graphing inequalities:
- < or > = dashed line
- ≤ or ≥ = solid line
- < or ≤ = shade below the line
- > or ≥ = shade above the line
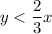
The slope of the first inequality is 2/3, therefore at x = 1, y = 2/3.
So the correct line for the first inequality is the dotted line with the shallower slope.
As the relation is < for this inequality, the shading should be below the dotted line.
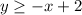
From inspection of the given graphs, the line of the second inequality (solid line) is the same in all graphs.
As the relation is ≥ for this inequality, the shading should be above the solid line.
Therefore, the only graph that satisfies these conclusions is graph D (attached).