Question

Match each interval with its corresponding average rate of change for q(x) = (x + 3)2.

1. -6 ≤ x ≤ -4
2. -3 ≤ x ≤ 0
3. -6 ≤ x ≤ -3
4. -3 ≤ x ≤ -2
5. -4 ≤ x ≤ -3
6. -6 ≤ x ≤ 0

A)-1
B)1
C)3
D)-3
E)0
F)-4

Answer 1

When we have a function:

f(x)

The average rate of change in the interval a < x < b

is given by:

`r = (f(b) - f(a))/(b - a)`

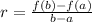
Now for each of the given intervals, let's find the average rate of changes.

q(x) = (x + 3)^2

1) -6 ≤ x ≤ -4

`r = ((-4 + 3)^2 - (-6 + 3)^2)/(-4 - (-6)) = (1 - 9)/(2) = -4`

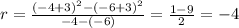
here the correct option is F.

2) -3 ≤ x ≤ 0

`r = ((0 + 3)^2 - (-3 + 3)^2)/(0 - (-3)) = (9)/(-3) = -3`

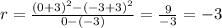
Here the correct option is D.

3) -6 ≤ x ≤ -3

`r = ((-3 + 3)^2 - (-6 + 3)^2)/(-3 - (-6)) = (9)/(3) = 3`

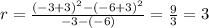
Here the correct option is C

4) -3 ≤ x ≤ -2

`r = ((-2 + 3)^2 - (-3 + 3)^2)/(-2 - (-3)) = (1)/(1) = 1`

Here the correct option is B.

5) -4 ≤ x ≤ -3

`r = ((-3 + 3)^2 - (-4 + 3)^2)/(-3 - (-4)) = -1/1 = -1`

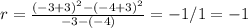
Here the correct option is A

6) -6 ≤ x ≤ 0

`r = ((0 + 3)^2 - (-6 + 3)^2)/(0 - (-6)) = (9 - 9)/(6) = 0`

Here the correct option is E.