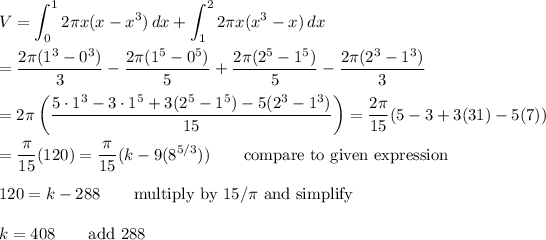Answer:
k = 408, as shown in your problem statement
Explanation:
Compute the integral in the usual way, then compare to the given expression and solve for k. We use the "cylindrical shell" method to find the volume.
The integral that gives the volume is ...