Question

Explanation: Zero Exponent

So far we have looked at powers of 10 with exponents greater than 0.
What would happen to our patterns if we included 0 as a possible exponent?

1. Write 10^12 × 10^0 with a power of 10 with a single exponent using the appropriate exponent rule. Explain or show your reasoning.

A. What number could you multiply 10^12 by to get this same answer?​

Answer 1

1) We can use the following property to simplify the product of powers as follows:

`a^(m)\cdot a^(n) = a^(m + n)`,
`a\in \mathbb{R}`,
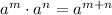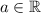`m,n\in \mathbb{Z}` (1)

Therefore, we have the following result:

`10^(12)\cdot 10^(0) = 10^(12+0) = 10^(12)`

A)
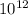`10^(12)` must be multiplied either by
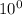`10^(0)` or by
`1` to get the same answer.

Explanation:

1) We can use the following property to simplify the product of powers as follows:

`a^(m)\cdot a^(n) = a^(m + n)`,
`a\in \mathbb{R}`,
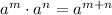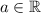`m,n\in \mathbb{Z}` (1)

Therefore, we have the following result:

`10^(12)\cdot 10^(0) = 10^(12+0) = 10^(12)`

A) In addition, we can use this property:

`(a^(m))/(a^(n)) = a^(m-n)`,
`a\in \mathbb{R}`,
`m,n\in \mathbb{Z}`

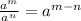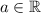We can apply the property mentioned above:

`10^(12)\cdot 10^(0) = 10^(12)\cdot (10^(n-n)) = 10^(12)\cdot \left((10^(n))/(10^(n)) \right) = 10^(12) \cdot 1 = 10^(12)`

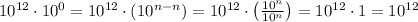
In consequence, we conclude that
`10^(0) = 1`.
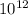`10^(12)` must be multiplied either by
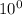`10^(0)` or by
`1` to get the same answer.