Question

Find the solution of the following simultaneous equations by the Cramer's method

2x+y-3z=-4
4x-2y+z=9
3x+5y-2z=5​

Answer 1

9514 1404 393

Answer:

(x, y, z) = (2, 1, 3)

Explanation:

Cramer's rule says you can find the solution by computing the determinants of the matrices obtained by replacing the corresponding variable coefficients with the constant vector.

The attached shows the resulting matrices for x, y, z and the unmodified coefficient matrix (at far right). The determinants of each are listed below, and the result of dividing the determinant for each variable by the determinant of the coefficient matrix is shown below that. In other words, ...

`\displaystyle x=\frac{\left|\begin{array}{ccc}-4&1&-3\\9&-2&1\\5&5&-2\end{array}\right| }{\left|\begin{array}{ccc}2&1&-3\\4&-2&1\\3&5&-2\end{array}\right| }=(-138)/(-69)=2`

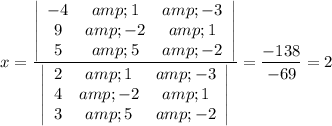
The other variable values are computed similarly.

The solution by Cramer's rule is (x, y, z) = (2, 1, 3).