Question

The equation for the ellipse given is 4x^2+9y^2-16x+18y-11​

Answer 1

a. a = 3, b = 2

b. The coordinate of the center is (2, -1)

c. The eccentricity of the ellipse is √5/3

d. Please see attached graph of the ellipse created with MS Excel

Explanation:

7. a. The given equation of the ellipse is presented as follows;

4·x² + 9·y² - 16·x + 18·y - 11

The general equation of an ellipse

`((x - h)^2)/(a^2) + ((y - k)^2)/(b^2) = 1`

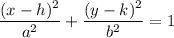
We can write;

4·x² - 16·x + 9·y² + 18·y - 11

4·(x² - 4·x + 4) + 9·(y² + 2·y + 1) - 25 - 11

4·(x² - 4·x + 4) + 9·(y² + 2·y + 1) = 25 + 11 = 36

4·(x - 2)² + 9·(y + 1)² = 36

`(4\cdot (x - 2)^2)/(36) + (9 \cdot (y + 1)^2)/(36) = (36)/(36)`

`\therefore ( (x - 2)^2)/(9) + ( (y + 1)^2)/(4) = ( (x - 2)^2)/(3^2) + ( (y + 1)^2)/(2^2) = 1`

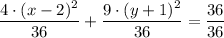
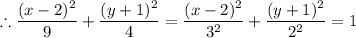
By comparison, a = 3, b = 2, h = 2, k = -1

b. The coordinate of the center, (h, k) = (2, -1)

c. The eccentricity of the ellipse = c/a

c² = a² - b²

∴ c² = 3² - 2² = 5

c = √5

Eccentricity = √5/3

d. Please find attached the graph of the ellipse created with MS Excel