Question

A tourist follows a passage that takes her 160 m west, then 180.m at an angle of 45.0∘ south of east, and finally 250 m at an angle 35.0∘ north of east. The total journey takes 12 minutes. (4)

a. Calculate the magnitude of her displacement from her original position.

b. She measures the distance she has walked to a precision of 5%. She times her total journey to ±20 s. (4)

(i) What is her average speed?

(ii) What is the absolute uncertainty on her absolute speed?

Answer 1

a) R = 172.82 m, 5.3 north of east b) v = (0.24 ± 0.01) m / s

Step-by-step explanation:

a) the displacement is a vector, so the easiest method to lock is looking for each component

let's start decomposing the vectors

x₁ = - 160 m

second shift

angle 45 south of east

cos (-45) = x₂ / d₂

sin (-45) = y₂ / d₂

x₂ = d₂ cos 45

y₂ = -d₂ sin 45

x₂ = 180 cos 45 = 127.28 m

y₂ = -180 sin 45 = - 127.28 m

third shift

cos 35 = x₃ / d₃

sin 35 = y₃ / d₃

x₃ = d₃ cos 35

y₃ = d₃ sin 35

x₃ = 250 cos 35 = 204.79 m

y₃ = 250 sin 35 = 143.39 m ₃

X axis

x_total = x₁ + x₂ + x₃

x_total = -160 +127.28 +204.79

x_total = 172.07 m

Y axis

y_total = y₁ + y₂ + y₃

y_total = 0 - 127.28 + 143.39

y_total = 16.11 m

to compose the displacement we use the Pythagorean theorem

R =
`√(x^2 +y^2)`

R =
`√(172.07^2 + 16.11^2 )`

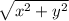
R = 172.82 m

in angle is

tan θ = y_total / x_total

ten θ = 16.11 / 172.07 = 0.0936

θ = tan⁻¹ 0.0936

θ = 5.3

angle is 5.3 north of east

b) the error in the distance is 5%,

e% = ΔR/R 100

ΔR = e% R / 100

ΔR = 5 172.82 / 100

ΔR = 8.6 m

the time error Dt = 20 s

We calculate the speed and this we calculate the error

v = R / t

v = 172.82 / 12 60

v = 0.240027 m / s

the error in this magnitude is

Δv =
`(dv)/(dR) \ \Delta R + (dv)/(dt) \ \Delta t`

Δv =
`(1)/(t) \ \Delta R + (R)/(t^2 ) \ \Delta t`

Δv =
`( 8.6)/(720) + (172.82 \ 20)/(720^2 )`

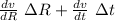
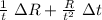
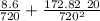
Δv = 0.013 m / s

the measurement result is

v = (0.24 ± 0.01) m / s