Question

Chuck has 20 feet of fencing and wishes to make a rectangular fence for his dog Rover. If he uses his house for one side of the fence what is maximum area?

Answer 1

50 square feet.

Explanation:

Let x represent the width of the fence and y represent the length of the fence.

One side of the length is already covered by the house. This leaves 2x and y. This must sum to 20. Hence:

`2x+y=20`

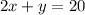
The area of the enclosure will be given by:

`A=xy`

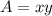
From the first equation, we can subtract 2x from both sides:

`y=20-2x`

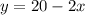
Substitute:

`A=x(20-2x)`

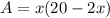
This is now a quadratic. Recall that the maximum value of a quadratic always occurs at its vertex. So, find the vertex of the equation. Distribute:

`A=20x-2x^2`

In this case, a = -2, b = 20, and c = 0.

Hence, the vertex is:

`\displaystyle x=-(b)/(2a)=-((20))/(2(-2))=5`

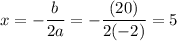
Substitute this value back into the equation and evaluate:

`A(5)=20(5)-2(5)^2=50\text{ ft}^2`

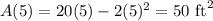
The maximum area is 50 square feet.

This occurs when the dimensions are 5 feet by 10 feet.