◇
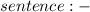
If two lines intersect, then the vertical angles formed are equal.
1) If the vertical angles are not equal, then lines do not intersect.
◇
2) If the two lines do not intersect, then the vertical angles are not equal.
◇

3) If the vertical angles are equal, then the two lines intersect.
◇