Question

Please help asap!! (even just one answer helps)

1. The combination locks on the lockers at a high school have numbers from 0 through 39 (inclusive). A locker combination consists of three different numbers, where the order matters. Because of the way the locks are made, all three numbers are even or all three numbers are odd. How many combinations are possible?

2. How many ways can you rearrange the letters in INFINITY?

3. Of the 30 students in a class, 11 practice taekwondo, 11 play piano, and 20 take dance lessons. 3 students play piano and take dance, 3 students do taekwondo and play piano, 5 students go to dance and practice taekwondo, and 3 students do none of these. How many students do all 3?

4. Our club has 10 members, and we need to appoint a president, a vice-president, and a secretary. How many ways can we do this if:

a) Each member can hold at most one office?
For this one I think you do

`(10!)/((10-3)!) = (10*9*8*7*6*5*4*3*2)/(7*6*5*4*3*2) = (10*9*8)/(1) = (720)/(1) = 720`
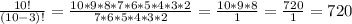
but I'm not entirely sure

b) Members can hold any number of offices?

Answer 1

Number 2 might be 3360