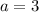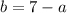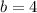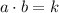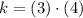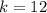Answer:
1) For
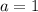 :
:
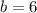 and
and
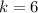 , 2) For
, 2) For
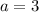 :
:
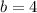 and
and
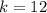
Explanation:
The polynomial
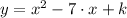 is a second-order polynomial of the form
is a second-order polynomial of the form
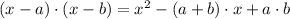 . By direct comparison, we construct the following system of equations:
. By direct comparison, we construct the following system of equations:
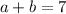 (1)
(1)
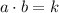 (2)
(2)
By (1) we know that there are a family of pairs such that the system of equations is satisfied. Let suppose that both
 and
and
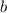 are integers. We assume two arbitrary integers for
are integers. We assume two arbitrary integers for
 :
:
1)
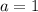
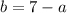
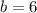
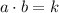
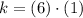
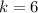
2)