Question

Write an exponential function in the form y=ab^x that goes through points (0,12) and (3,6144)

Answer 1

Given:

An exponential function goes through points (0,12) and (3,6144).

To find:

The exponential function.

Solution:

The general exponential function is:

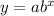`y=ab^x` ...(i)

The function goes through point (0,12). Substituting
`x=0,y=12`, we get

`12=ab^0`

`12=a`

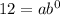
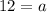
The function goes through point (3,6144). Substituting
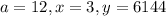`a=12, x=3,y=6144` in the general exponential function, we get

`6144=12b^3`

`(6144)/(12)=b^3`

`512=b^3`

`512^{(1)/(3)}=b`

`8=b`

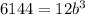
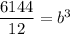
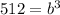
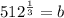
Putting
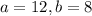`a=12,b=8` in (i), we get

`y=12(8)^x`

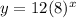
Therefore, the required exponential function is
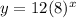`y=12(8)^x`.