Answer:
y(t) = 3u₂(t) [
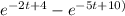 ] - 4u₅(t) [
] - 4u₅(t) [
 ]
]
Explanation:
To find - y″+ 5y′ + 6y = 3δ(t − 2) − 4δ(t −5); y(0) = y′(0) = 0
Formula used -
L{δ(t − c)} =
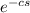
L{f''(t) = s²F(s) - sf(0) - f'(0)
L{f'(t) = sF(s) - f(0)
Solution -
By Applying Laplace transform, we get
L{y″+ 5y′ + 6y} = L{3δ(t − 2) − 4δ(t −5)}
⇒L{y''} + 5L{y'} + 6L{y} = 3L{δ(t − 2)} − 4L{δ(t −5)}
⇒s²Y(s) - sy(0) - y'(0) + 5[sY(s) - y(0)] + 6Y(s) = 3
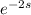 - 4
- 4
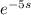
⇒s²Y(s) - 0 - 0 + 5[sY(s) - 0] + 6Y(s) = 3
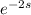 - 4
- 4
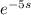
⇒s²Y(s) + 5sY(s) + 6Y(s) = 3
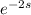 - 4
- 4
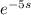
⇒[s² + 5s + 6] Y(s) = 3
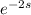 - 4
- 4
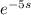
⇒[s² + 3s + 2s + 6] Y(s) = 3
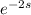 - 4
- 4
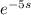
⇒[s(s + 3) + 2(s + 3)] Y(s) = 3
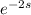 - 4
- 4
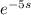
⇒[(s + 2)(s + 3)] Y(s) = 3
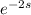 - 4
- 4
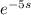
⇒Y(s) =
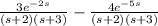
Now,
Let
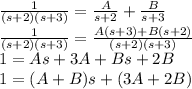
By Comparing, we get
A + B = 0 and 3A + 2B = 1
⇒A = -B
and
3(-B) + 2B = 1
⇒-B = 1
⇒B = -1
So,
A = 1
∴ we get
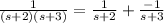
So,
Y(s) =
![3e^(-2s)[ (1)/((s + 2)) - (1)/((s + 3))] - 4e^(-5s)[ (1)/((s + 2)) - (1)/((s + 3))]](https://img.qammunity.org/2022/formulas/mathematics/college/oj38hyw2ix5793pa5rw6s70hmzgzb1zkfa.png)
⇒Y(s) =

By applying inverse Laplace , we get
y(t) = 3u₂(t) [
 ] - 4u₅(t) [
] - 4u₅(t) [
 ]
]
⇒y(t) = 3u₂(t) [
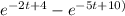 ] - 4u₅(t) [
] - 4u₅(t) [
 ]
]
It is the required solution.