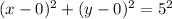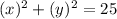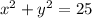Question

Find the equation of a circle that is centered at the origin and is tangent to the circle (x−6)^2+(y−8)^2=25

Answer 1

Center: ( 6 , 8 )

Radius: 5

Answer 2

`x^2 +y^2 = 25`

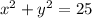
Explanation:

Center of the required circle = (0, 0)

Center of the given circle = (6, 8)

Radius of the given circle = 5 units

Distance between the centers of both the circles

`=√((6-0)^2 +(8-0)^2)`

`=√((6)^2 +(8)^2)`

`=√(36 +64)`

`=√(100)`

`=10\: units`

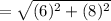
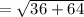
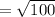
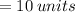
Since, required circle is tangent to the given circle with radius 5 units.

Therefore,

Radius of required circle = 10 - 5 = 5 units

Now, Equation of required circle can be obtained as:

`(x - 0)^2 +(y - 0)^2 = 5^2`

`(x)^2 +(y)^2 = 25`

`x^2 +y^2 = 25`