Explanation:
Given that,
The height of the cylinder, h = 3x-4
The radius of the cylinder, r = 3x+2
The volume of the cylinder is :
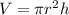
The surface area of the cylinder is :
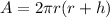
The ratio of the volume of the cylinder to the surface area of the cylinder is :
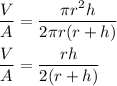
Put all the values,
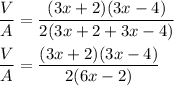
Hence, this is the required solution.