Question

A student needs to select 3 books from 3 different mathematics, 3 different physics and 1 history books. What is the probability one of them is mathematics and other two are either physics or history books

Answer 1

Probability that one of them is mathematics and other two are either physics or history books = 0.51

Explanation:

Given - A student needs to select 3 books from 3 different mathematics, 3 different physics and 1 history books.

To find - What is the probability one of them is mathematics and other two are either physics or history books ?

Solution -

Given that,

A student needs to select 3 books from 3 different mathematics, 3 different physics and 1 history books.

So,

Total number of books = 3 + 3 + 1 = 7

The student has to select 3 books

So, Total number of ways =
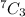`^(7) C_(3)` = 35

So,

Probability that one of them is mathematics and other two are either physics or history books is -

=
`(^(3) C_(1). ^(4) C_(2) )/(^(7) C_(3))`

=
`((3)(6))/(35)`

=
`(18)/(35)`

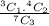
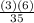
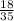
= 0.51

⇒Probability that one of them is mathematics and other two are either physics or history books = 0.51