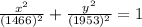Question

A satellite is to be put into an elliptical orbit around a moon as shown below. A vertical ellipse is shown surrounding a spherical object labeled, moon. The moon is a sphere with radius of 1000 km. Determine an equation for the ellipse if the distance of the satellite from the surface of the moon varies from 953 km to 466 km.

Answer 1

The correct equation will be "
`(x^2)/((1466)^2) +(y^2)/((1953)^2) =1`".

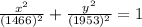Explanation:

In the above question, the figure is missing. Please find below the attachment of the figure.

According to the question,

Radius of a moon,

r = 1000 km

The max. distance from moon's surface to the satellite,

a = 953 km

The min. distance from moon's surface to the satellite,

b = 466 km

Now,

As per the question or the diagram,

⇒
`a_1=a+r`

`=953+1000`

`=1953 \ km`

⇒
`b_1=b+r`

`=466+1000`

`=1466 \ km`

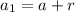
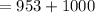
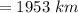
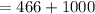
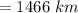
hence,

The equation of ellipse will be:

⇒
`(x^2)/(b_1^2) +(y^2)/(a_1^2) =1`

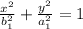
On substituting all the values, we get

⇒
`(x^2)/((1466)^2) +(y^2)/((1953)^2) =1`