Question

A plane flying with an air speed of 300 mph at 50 degrees and it crosses the jet stream, which is blowing at 200 mph at an angle of 160 degrees. The plane's actual velocity with respect to the ground is the vector sum of these two velocities. Find the actual velocity to the nearest whole mph and degree (add the sum of the vectors).

Answer 1

298.24 mph at an angle of 89 degrees

Explanation:

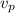`v_p` = Velocity of plane = 300 mph at 50 degrees

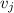`v_j` = Velocity of jet stream = 200 mph at 160 degrees

The velocity of the plane in component form is

`v_p=300\cos50^(\circ)\hat{i}+300\sin50^(\circ)\hat{j}`

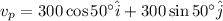
The velocity of the jet stream in component form is

`v_j=200\cos160^(\circ)\hat{i}+200\sin160^(\circ)\hat{j}`

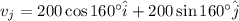
Resultant velocity is given by

`v=(300\cos50^(\circ)+200\cos160^(\circ))\hat{i}+(300\sin50^(\circ)+200\sin160^(\circ))\hat{j}\\\Rightarrow v=4.9\hat{i}+298.2\hat{j}`

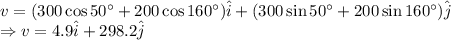
Magnitude is given by

`|v|=√(4.9^2+298.2^2)\\\Rightarrow |v|=298.24\ \text{mph}`

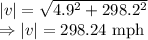
Angle is given by

`\theta=\tan^(-1)(298.2)/(4.9)=89^(\circ)`

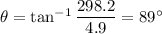
The velocity of the plane is 298.24 mph at an angle of 89 degrees.