Question

Graph: Y-3 = 1/2 (x + 2)

Answer 1

Move all terms not containing y to the right side of the

equation.

y= X/2+4

Rewrite in slope-intercept form.

y=1/2x+4

Use the slope-intercept form to find the slope and y

intercept.

Slope: 1/2

y-intercept: (0,4)

Any line can be graphed using two points. Select two x values, and plug them into the equation to find the corresponding y values. Answer: (0,4) (2,5)

Answer 2

The graph should look like a line with a slope of
`\((1)/(2)\)` passing through the point (0, 4).

To graph the equation
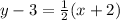`\(y - 3 = (1)/(2)(x + 2)\)`, we can start by rewriting it in slope-intercept form
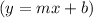`(\(y = mx + b\))`, where
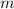`\(m\)` is the slope and
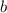`\(b\)` is the y-intercept.

`\[y - 3 = (1)/(2)(x + 2)\]`

Distribute the
`\((1)/(2)\)` on the right side:

`\[y - 3 = (1)/(2)x + 1\]`

Now, add 3 to both sides to isolate \(y\):

`\[y = (1)/(2)x + 4\]`

Now, you can see that the slope
`(\(m\))` is
`\((1)/(2)\)`, and the y-intercept
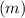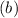`(\(b\))` is 4.

To graph this equation, plot the y-intercept at (0, 4) and use the slope to find additional points. For example, if you move one unit to the right (increase x by 2), you would move up
`\((1)/(2)\)` units. Connect these points to draw the line.

Therefore the graph should look like a line with a slope of
`\((1)/(2)\)`passing through the point (0, 4).