Question

At which value(s) of x does the graph of the function F(x) have a vertical asymptote? Check all that apply.

F(x) = x/(x+2)(x-1)

o x=10
o x=-2
o x=0
o x=-1
o x=2
o x=1

Answer 1

x = - 2, x = 1

Explanation:

Given

f(x) =
`(x)/((x+2)(x-1))`

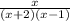
The denominator cannot be zero as this would make f(x) undefined.

Equating the denominator to zero and solving for x gives the values that x cannot be and if the numerator is non zero for these values then they are vertical asymptotes.

(x + 2)(x - 1) = 0

x + 2 = 0 ⇒ x = - 2

x - 1 = 0 ⇒ x = 1

Vertical asymptotes occur at x = - 2 and x = 1