Answer:
Explanation:
Given :-
And we need to prove that ,
So let us assume that ,
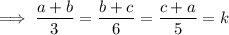
Where k is a constant . Now equate each of the three terms separately to k . Therefore we have ,
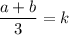
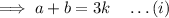
Similarly we can say that ,
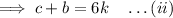
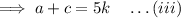
Subtracting (i) and (ii) :-

Adding (iv) and (iii) :-
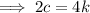

Put this is (ii) :-
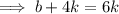
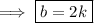
Similarly we will get ,
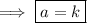
Proving the given equation :-
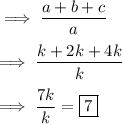
Hence proved !