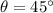Answer:
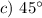
Explanation:
Given
A semicircle divided into 8 parts
Required
Angle that can be measured with the piece
First, we calculate the minimum angle that can be calculated.
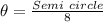
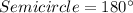
So, we have:
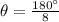
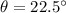
This implies that all angles that can be measured using the piece must be a multiple of 22.5 not greater than 180 degrees (i.e. not greater than the semicircle)
So, we have:
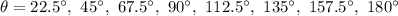
From the list of options, only 45 degrees appear in the possible values of
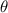
Hence: