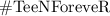Question 1.) Find Probability :
A. A red card or a spade .
Total red cards = total hearts + total diamonds
Total spades = 13 cards
- Favourable outcomes = 26 + 13 = 39
now, probability of getting either A red card or a spade is :
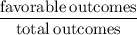
B. A face card or an ace
- total face cards = 4 × 3 = 12
favorable outcomes = 12 + 4 = 16
The probability of getting a face card or an ace :
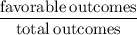
C. A diamond and a 9
We know there's only one diamond which is 9
So, favourable outcome = 1
Now, probability of getting a diamond and a 9 :
_____________________________
2.) Two pair of dice is rolled. Determine the probability :
The outcomes are :
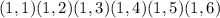


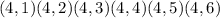
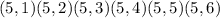

Total number of outcomes = 6² = 36 outcomes
Find :
A. P (sum is 4 or 11 )
Total number of outcomes having sum of 4 is :
Total number of outcomes having sum of 11 is :
So, favorable outcome = 2 + 3 = 5
Probablity ( sum is 4 or 11 ) :
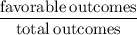
B. P(sum is less than 5 or sum is greater than 8)
Total number of outcomes having sum less than 5 is :
Total number of outcomes having sum greater than 8 is :
So, favorable outcomes = 10 + 6 = 16
Probablity of (sum is less than 5 or sum is greater than 8) is :
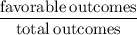
_____________________________