Answer:
They are not inverse functions
Explanation:
Given
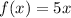
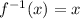
Required
Determine if both are inverse functions
First calculate the inverse of f(x)
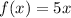
Replace f(x) with y
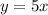
Swap x and y
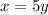
Make y the subject
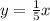
Replace y with f-1(x)
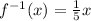
By comparison:
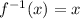 and
and
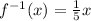 are not the same:
are not the same:
Hence:
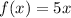 and
and
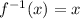 are not inverse functions
are not inverse functions