Answer:
a) The angle of refraction is approximately 34.7
b) The angle the light have to be incident to give an angle of refraction of 90° is approximately 53.42°
Step-by-step explanation:
According to Snell's law, we have;
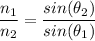
The refractive index of the glass, n₁ = 1.66
The angle of incident of the light as it moves into water, θ₁ = 27.2°
a) The refractive index of water, n₂ = 1.333
Let θ₂ represent the angle of refraction of the light in water
By plugging in the values of the variables in Snell's Law equation gives;
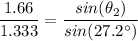
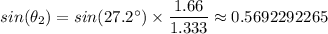
θ₂ = arcsin(0.5692292265) ≈ 34.7°
The angle of refraction of the light in water, θ₂ ≈ 34.7°
b) When the angle of refraction, θ₂ = 90°, we have;
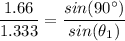
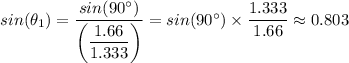
θ₁ ≈ arcsin(0.803) ≈ 53.42°
The angle of incident, θ₁, that would give an angle of refraction of 90° is θ₁ ≈ 53.42°