Answer:
To decide whether to add or subtract, determine if the values of the coefficients are the same or opposites:
. If the values are the same, subtract the equations.
• If the values are opposites or additive inverses, add the equations.
Explanation:
Given
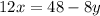
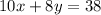
Required
How to solve
Options (1) and (2) are incorrect because none of the options eliminate x or y.
For option (3),
- Check for the coefficients of x and y
- If they are the same (sign and value), then subtract; otherwise add
For instance:
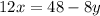
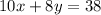
Rewrite the second equation
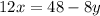
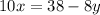
The coefficient of y are the same, so we subtract;
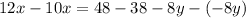
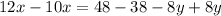

See that y has been eliminated