Answer:
The sum of the first 13 terms of the sequence is -67,108,863.
Explanation:
Sum of the first n terms of a geometric sequence:
The sum of the first n terms of a geometric sequence, with first term
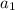 and ratio r, is given by:
and ratio r, is given by:
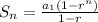
In this question:

Sum of the first 13 terms:
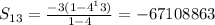
The sum of the first 13 terms of the sequence is -67,108,863.