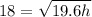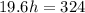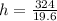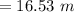Question

A ball is throw into the sky at 18m/s. How high can it reach?

Answer 1

The maximum height of the ball will be "16.53 m".

Step-by-step explanation:

Given that,

`V_(final) = 18 \ m/s`

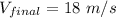
As we know,

The initial as well the final height on the ball will be same after it reaches it's maximum height.

then,

⇒
`V_(final)=V_(initial)`

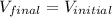
where,
`V_(initial) = √(2gh)`

`=√(2* 9.8* h)`

`=√(19.6h)`

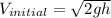
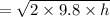
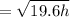
hence,

The max height of the ball will be:

⇒
`18=√(19.6h)`

`19.6h=324`

`h=(324)/(19.6)`

`=16.53 \ m`