Question

Find the zeros of the quadratic equation f(x)= 6x²-3, and verify the relation between its zeros and coefficients.

using the formula
alpha+beta= -b/a
alpha × beta = c/a​

Answer 1

Answer:

Explanation:

We are already given the following formulas :-

`\blue{\alpha + \beta = (-b)/(a)}`

`\red{\alpha * \beta = (c)/(a)}`

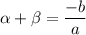
Given that the polynomial is :-

`\sf{6x^2 + 0x - 3}`

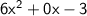
Now, we will use factorisation as our first weapon :-

6x² -3 = 0 [As we have to find the zeroes of the equation]

6x² = 3

x² =
`(3)/(6)`

x² =
`(1)/(2)`

x =
`(1)/(√(2))`

Now, we can take one zero as 1/Root 2 and other -1/root 2

`(1)/(√(2)) + (-1)/(√(2)) | (0)/(6) = 0`

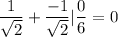
0 |0 Hence verified.

`(1)/(√(2)) * (-1)/(√(2)) | (-3)/(6) = 0`

`(1)/(2) | (1)/(2)`

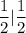
Hence, proved.