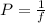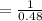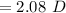Question

A person has a far point of 50 cm. If he is wearing glasses 2 cm from the eyes, determine

the power of the lens needed for him to see distant object clearly.​

Answer 1

The power will be "2.08 D".

Step-by-step explanation:

According to the question,

The location of the image form lens,

`d_i=50-2`

`=48 \ cm`

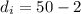
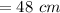
We know that,

⇒
`(1)/(d_i) -(1)/(d_o) =(1)/(f)`

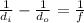
here,

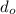`d_o` = Object location

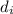`d_i` = Image location

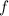`f` = Focal length

On putting the values in the above expression, we get

⇒
`(1)/(48) -(1)/(\infty) =(1)/(f)`

`f=48 \ cm`

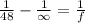
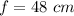
or,

`f=0.48 \ m`

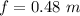
hence,

The refractive power will be:

⇒
`P=(1)/(f)`

`=(1)/(0.48)`

`=2.08 \ D`