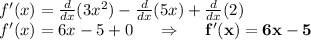Answer:
La derivada de la función es:
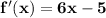
Explanation:
Recordemos que la derivada de
- Una suma es igual a la suma de las derivadas:
![[a + b + c]'=[a]'+[b]'+[c]'](https://img.qammunity.org/2022/formulas/mathematics/high-school/h6cgem1tla7ubk5ssujftr236msw6n49nr.png)
- Una constante es cero:
![[k]'=0\;\;,\;\;\;\;\text{si}\;\;k=\text{constante}](https://img.qammunity.org/2022/formulas/mathematics/high-school/h4qax353m6oa00ndxunt73lj9afb2fadp4.png)
- Un producto es:
![[ab]' = [a]'b + a[b]'](https://img.qammunity.org/2022/formulas/mathematics/high-school/32wfzalfkch3nujy1zs9b27lgw46pgzxb8.png)
- Una potencia:
![[a^n]'=na^(n-1)](https://img.qammunity.org/2022/formulas/mathematics/high-school/xzt8qn5kxvrnhl8vzaa1atl8cgwr89p3uk.png)
La derivada de la función
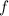 con respecto a
con respecto a
 es definida como
es definida como
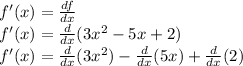
donde
Por lo tanto,