Question

What is an equation of the line that passes through the points (1, 1) and (7, -5)?

Answer 1

y = -1 x + 2

Explanation:

First of all, remember what the equation of a line is:

y = mx+b

m is the slope, and b is the y-intercept.

Now, to find m, simply substitue here:
`m=(y1-y2)/(x1-x2)`

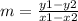
Which means: m =
`(-5-1)/(7-1) = -1`

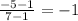
Now, look at our line's equation so far: y=-1x+b.

b is what we want, the -1 is already set and x and y are just two "free variables" sitting there. We can plug anything we want in for x and y here, but we want the equation for the line that specfically passes through the two points (1,1) and (7,-5).

So, why not plug in for x and y from one of our (x,y) points that we know the line passes through? This will allow us to solve for b for the particular line that passes through the two points you gave!

You can use either (x,y) point you want..the answer will be the same:

Either: (1,1). y=mx+b or 1=-1 × 1+b, or solving for b: b=1-(-1)(1). b=2.

Or: (7,-5). y=mx+b or -5=-1 × 7+b, or solving for b: b=-5-(-1)(7). b=2.

both gave us the same answer for b, which is 2.

Therefore, the equation of the line that passes through the points (1,1), and (7,-5) is:

Y = -x + 2

Answer 2

y=-x+2

Explanation:

m=(y2-y1)/(x2-x1)

m=(-5-1)/(7-1)

m=-6/6

m=-1

y-y1=m(x-x1)

y-1=-1(x-1)

y-1=-x+1

y=-x+1+1

y=-x+2