Question

A quadratic equation is shown below: x2 − 8x + 13 = 0 Which of the following is the first correct step to write the above equation in the form (x − p)2 = q, where p and q are integers? (5 points) Subtract 5 from both sides of the equation Subtract 3 from both sides of the equation Add 5 to both sides of the equation Add 3 to both sides of the equation

Answer 1

Add 3 to both sides of the equation

Solution:

The first step is to basically realize that all it's asking you to do is to find a way to make the expression on the left (
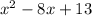`x^2 - 8x + 13`) into an expression that is a perfect square. So what number should you add to both sides such that
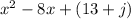`x^2 - 8x + (13 + j)` can be factored into
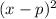`(x-p)^2` ? Well, we can approach it like this:

Since
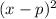`(x-p)^2` can be turned into
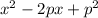`x^2 -2px + p^2`, and our original form was
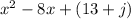`x^2 - 8x + (13 + j)`, we quickly realize that
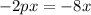`-2px = -8x`. From there, we can easily tell that
`p = 4`

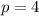
Plug this into our last value
`p^2` to get 16. Therefore, if we compare this with our original equation again
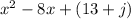`x^2 - 8x + (13 + j)`, we notice that 13 + j = 16.

Thus, j = 3 for the last answer.

Add 3 to both sides of the equation.

Note: With more practice, you will quickly gain enough intuition to notice that
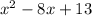`x^2 - 8x + 13` is very close to
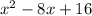`x^2 - 8x + 16` which can be factored into
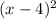`(x-4)^2`. But for now, the solution above will suffice. I hope this helps :))