Question

In the function, f(x) = 3 − sin(x + π), three transformations have been applied. Briefly describe the three transformations.

Answer 1

The three transformations used are -

Vertical shift

Phase shift

Period

Explanation:

Given - Given the function, f(x) = 3 − sin(x + π)

To find - In the function, three transformations have been applied. Briefly describe the three transformations.

Proof -

Given that, The function is f(x) = 3 − sin(x + π)

We know the

The general form of sine function is -

y = Asin(Bx + C) + D

where

A is the Amplitude

The period is
`(2\pi )/(B)`

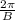
Phase (Horizontal) shift is C

Vertical Shift id D

Here, The function is f(x) = 3 − sin(x + π)

By Comparing with General form of sin function, we get

-1 is the Amplitude

The period is 2
`\pi`

Phase (Horizonal) shift is
`\pi`

Vertical shift is 3

The three transformations used are -

Vertical shift

Phase shift

Period