Question

Scott strikes out at bat 36% of the time. Find the probability that he strikes out no more than three times on his next eight times at bat.

Answer 1

68.47%

Explanation:

The answer is 68.47%

Solution -

We know that,

The binomial formula is -

P(x) =
`^(n)C_(x)p^(x)q^(n-x)`

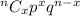
where

n is the number of trials

x is the strike out number.

p is the probability of success

q is the probability of failure

Here,

n = 8

p = 36% = 0.36

q = 1 - 0.36 = 0.64

Now,

We want to find the probability that he strikes out no more than 3 times (i.e. <= 3.)

So,

We need to check the cases where x = 0, 1, 2 and 3.

Now,

For x = 0,

P(0) =
`^(8)C_(0)(0.36)^(0)(0.64)^(8-0)` = (0.64)⁸

P(1) =
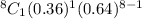`^(8)C_(1)(0.36)^(1)(0.64)^(8-1)` = 8×0.35×0.64⁷ .

P(2) =
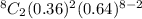`^(8)C_(2)(0.36)^(2)(0.64)^(8-2)` = 28×0.35² ×0.64⁶ .

P(3) =
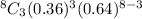`^(8)C_(3)(0.36)^(3)(0.64)^(8-3)` = 56×0.35³ ×0.64⁵ .

So,

Probability that he strikes out no more than three times = P(0) + P(1) + P(2) + P(3) = 68.47%