Question

The polynomial of degree 4, P(x) has a root of multiplicity 2 at x=1 and roots of multiplicity 1 at x=0 and x=-3. It goes through the point (5,256)

Answer 1

P(x) = (
`(2)/(5)`)x(x + 3)(x - 1)²

Explanation:

Given - The polynomial of degree 4, P(x) has a root of multiplicity 2 at x=1 and roots of multiplicity 1 at x=0 and x=-3. It goes through the point (5,256)

To find - Formula for P(x) ?

Proof -

Given that,

P(x) has a root of multiplicity 2 at x=1

So,

(x - 1)² is a factor.

Now,

Given that, there is roots of multiplicity 1 at x=0 and x=-3

So,

(x - 0) and ( x - (-3) are also factor

So,

P(x) can be written as

P(x) = Ax(x + 3)(x - 1)² .........(1)

where A is a constant.

Now,

Given that, It goes through the point (5,256)

⇒At x = 5, P(x) = 256

So,

Put the values of x and P(x) in equation (1), we get

P(x) = Ax(x + 3)(x - 1)²

⇒256 = A(5)(5 + 3)(5 - 1)²

⇒256 = 5A(8)(4)²

⇒256 = 40A(16)

⇒256 = 640 A

⇒A =
`(256)/(640)` =
`(2)/(5)`

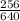∴ we get

P(x) = (
`(2)/(5)`)x(x + 3)(x - 1)²