Question

A spinner has regions numbered 1 through 18. What is the probability that ___________________

the spinner, spun once, will stop on an even number or a multiple of 3?

Answer 1

Probability that the spinner stop on an even number or a multiple of 3 =
`(2)/(3)`

Explanation:

Given - A spinner has regions numbered 1 through 18.

To find - What is the probability that the spinner, spun once, will stop on an even number or a multiple of 3?

Solution -

Given that,

A spinner has regions numbered 1 through 18.

So,

The sample space, S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18}

i.e.

n(S) = 18

Now,

Let A be the outcomes that gives even number or a multiple of 3,

Then

A = {2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18}

i.e.

n(A) = 12

∴ we get

Probability that the spinner stop on an even number or a multiple of 3 =
`(n(A))/(n(S))`

=
`(12)/(18)`

=
`(2)/(3)`

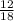
i.e.

Probability that the spinner stop on an even number or a multiple of 3 =
`(2)/(3)`